Ultrafast Electron Dynamics
The emergence of tools for attosecond measurement allows the experimental study of the dynamics of electrons and nuclei in molecules, on the attosecond (1 as = 10-18 s) time scale.
Such short pulses have a broad spectral bandwidth, leading to the coherent population of several electronic states, thus breaking the Born–Oppenheimer approximation. As a result, the system is no longer confined to be in a single stationary electronic state butis now a superposition of electronic states, called an electronic wave packet:this superposition is non-stationary, i.e. its probability density is time-dependent. Such electron dynamics is often called charge migration in the literature. For an isolated static molecular geometry where the pulse creates a superposition of two states, the period of oscillation of the electron density is related to the energy gap between the populated eigenstates: T = h/(E1-E0).
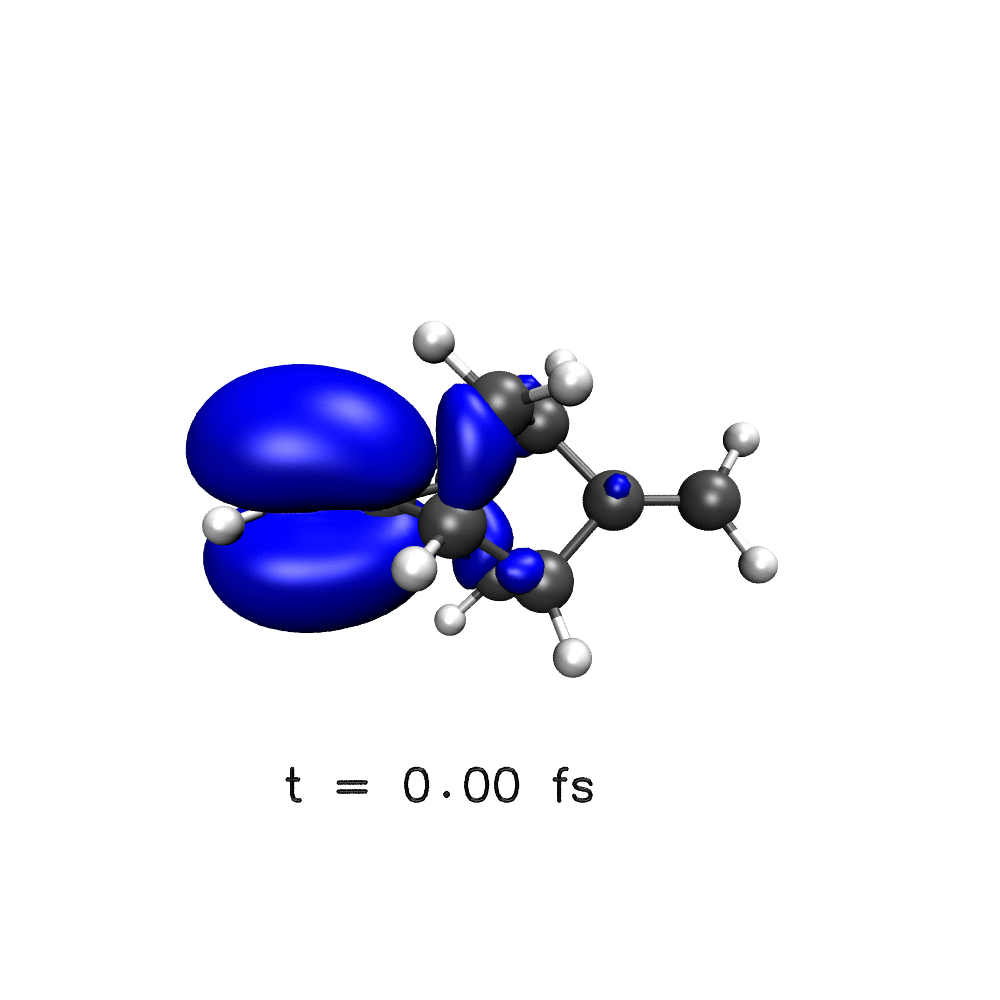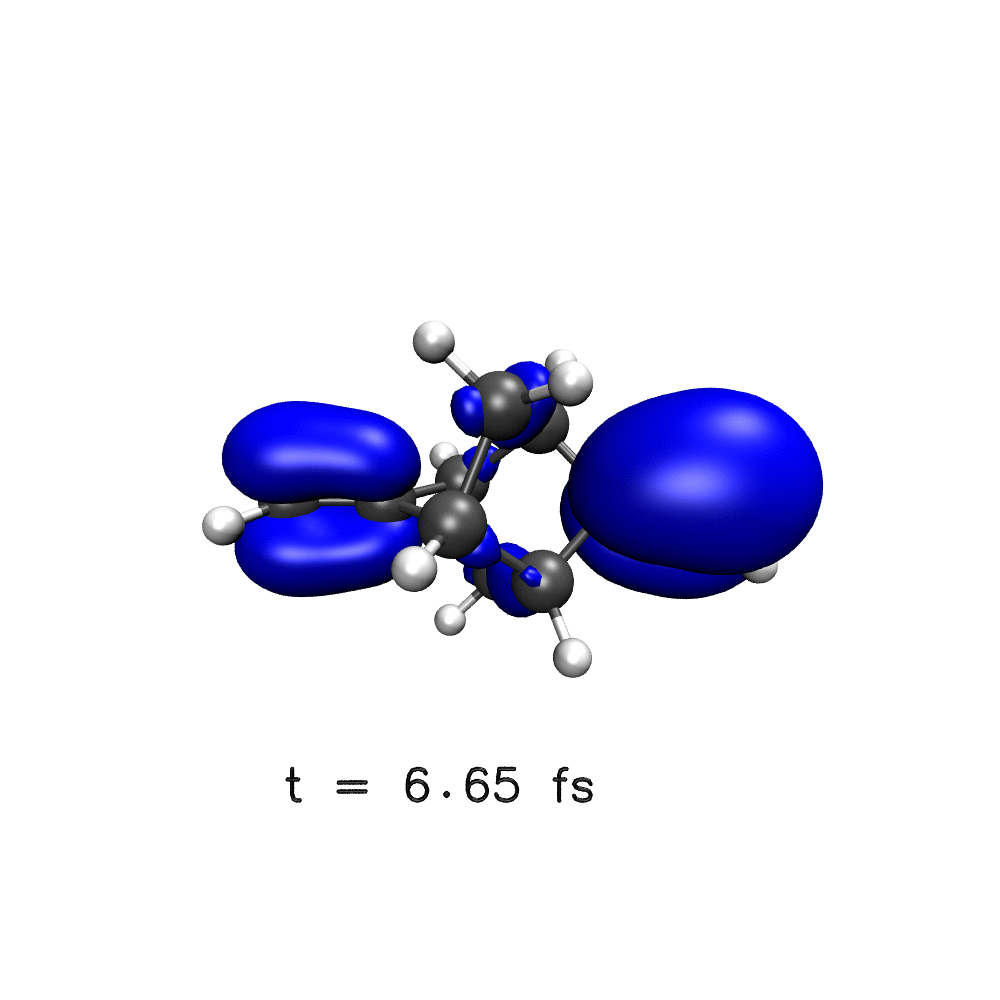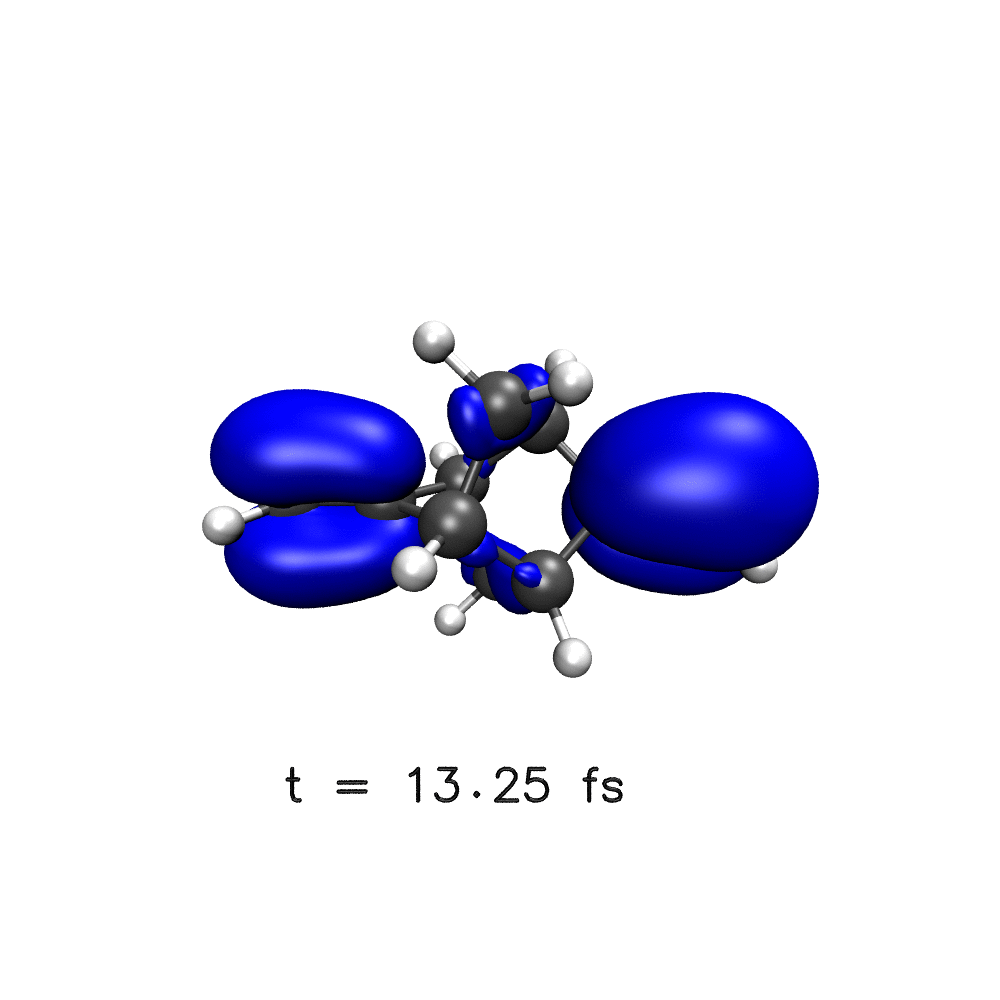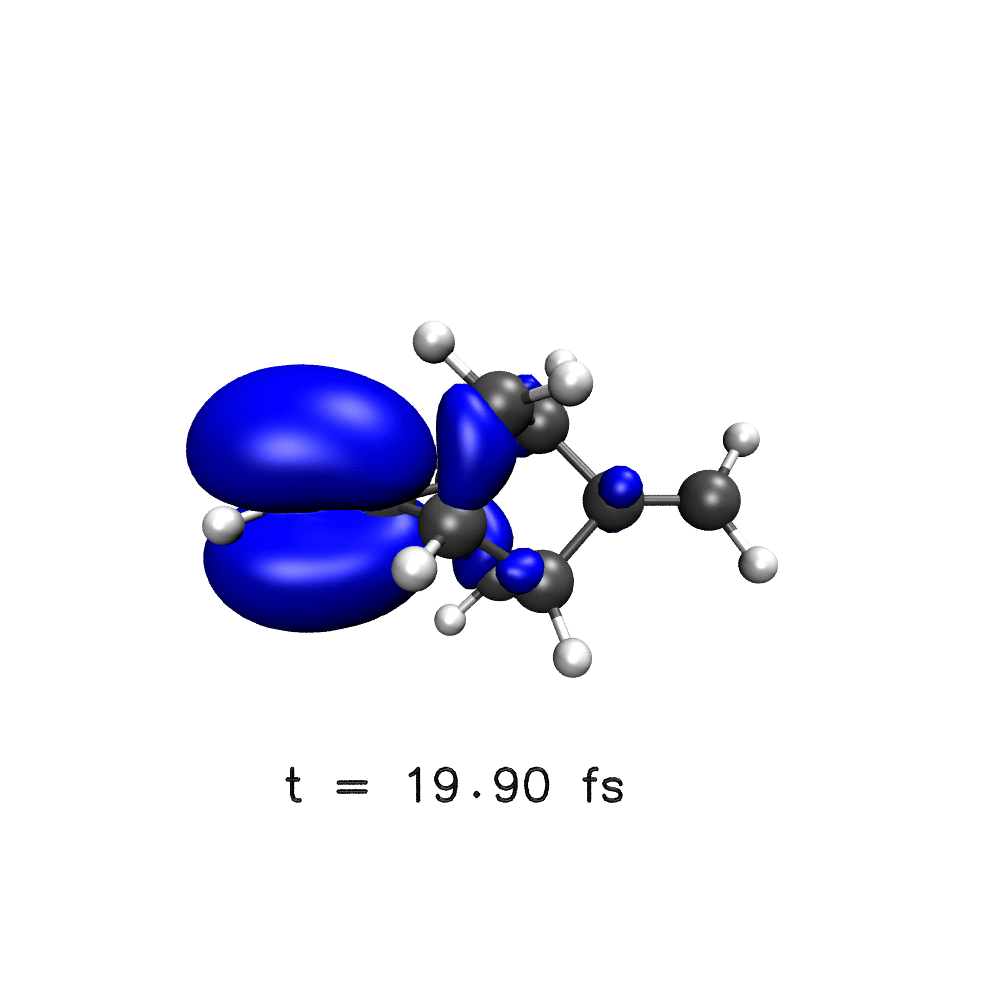
One key target of attosecond experiments remains the real-time observation of electron dynamics upon ionisation in molecules, where changes in both the electronic density and the nuclear geometry are expected.
Molecular charge migration is still often treated as a purely electronic process, solving the electronic time-dependent Schrodinger equation at a single fixed nuclear geometry. This neglects the effects of i) the motion of the nuclei, and ii) the natural spatial delocalisation of the nuclei due to the zero-point energy.
Nuclear wave packet delocalisation is due to the zero-point energy, the nuclei undergo fluctuations in their positions even in the molecular ground state. The various nuclear geometries within the nuclear wavepacket lead to a distribution of energy gaps and therefore of oscillation periods in the electronic density. The oscillations will then dephase with time, calling into question the commonly held picture of long-lived electronic oscillations at a well-defined frequency. Using a simple analytical model, we have shown that electron dynamics dephases faster when the nuclear wave packet is wider and when the difference of slopes of the potential energy surfaces involved is greater1.
Using a distribution on nuclear geometries (sampled from a Wigner distribution), we have shown that nuclear spatial delocalisation, neglected in the single-geometry approximation, leads to the rapid dephasing of electron dynamics in para-xylene1, phenylalanine derivative2, polycyclic-norbornadiene1,3, modified adamantane4 and glycine5 cations on a few femtosecond time scale. We also highlight the features that would lead to longer dephasing times, such as narrow wavepacket width and small gradient difference, and through our simulations,suggest a system in which long-lived electron dynamics may be observed – a two-ringed norbornadiene3.
We have also shown the effect of nuclear spatial delocalisation to have a much greater affect on electron dynamics than nuclear motion2,4,5, treated using the mixed quantum-classical Ehrenfest dynamics method6, and have included both effects simultaneously4,5.
Our method of treating nuclear spatial delocalisation with and without classical nuclear motion has been compared to fully quantum mechanical simulations using the DD-vMCG method for para-xylene, by Vacher et al.7, giving similar results and dephasing times for electron dynamics. This validates our approach, which is applicable to larger systems than DD-vMCG and to systems containing several electronic states of interests. This, and further work by M. Vacher, has been collated and summarised in a recent book chapter8.
- M. Vacher, L. Steinberg, A. J. Jenkins, M. J . Bearpark, M. A. Robb, “Electron dynamics following photoionization: Decoherence due to the nuclear-wave-packet width” Phys. Rev. A, 92, 040502(Rapid Communication) (2015) https://doi.org/10.1103/PhysRevA.92.040502 PDF
- A. J. Jenkins, M. Vacher, M. J. Bearpark, M. A. Robb, “Nuclear spatial delocalization silences electron density oscillations in 2-phenyl-ethyl-amine (PEA) and 2-phenylethyl-N,N-dimethylamine (PENNA) cations” J. Chem. Phys., 144, 104110 (2016) https://doi.org/10.1063/1.4943273 PDF
- A. J. Jenkins, M. Vacher, R. M. Twidale, M. J. Bearpark, M. A. Robb, “Charge migration in polycyclic norbornadiene cations: Winning the race against decoherence” J. Chem. Phys., 145, 164103 (2016) http://dx.doi.org/10.1063/1.4965436 PDF Supplementary
- M. Vacher, F. E. A. Albertani, A. J. Jenkins, I. Polyak, M. J. Bearpark, M. A. Robb, “Electron and nuclear dynamics following ionisation of modified bismethylene-adamantane” Faraday Discuss., 194, 95-115 (2016) http://dx.doi.org/10.1039/C6FD00067C (Pre-Print/Accepted Version)
- I. Polyak, A. J. Jenkins, M. Vacher, M. E. F. Bouduban, M. J. Bearpark, M. A. Robb, “Charge migration engineered by localisation: electron-nuclear dynamics in polyenes and glycine” Mol. Phys., 116, 2474-2489 (Michael Baer Festschrift) (2018) https://doi.org/10.1080/00268976.2018.1478136 PDF
- M. Vacher, M. J. Bearpark, M. A. Robb, J. P. Malhado, “Electron Dynamics upon Ionization of Polyatomic Molecules: Coupling to Quantum Nuclear Motion and Decoherence” Phys. Rev. Lett., 118, 083001 (2017)
- M. Vacher, D. Mendive-Tapia, M. J. Bearpark, M. A. Robb “The second-order Ehrenfest method: A practical CASSCF approach to coupled electron-nuclear dynamics” Theoretical Chemistry Accounts, 133, 1505 (2014)
- M. A. Robb, A. J. Jenkins, M. Vacher, “How Nuclear Motion Affects Coherent Electron Dynamics in Molecules” in “Attosecond Molecular Dynamics”, Eds. M. J. J. Vrakking & F. Lepine, Royal Society of Chemistry, 2018, p275-305 http://dx.doi.org/10.1039/9781788012669
Quantum Ehrenfest
We have detailed an algorithm for quantum dynamics where an Ehrenfest potential is combined with fully quantum nuclear motion (Quantum-Ehrenfest, Qu-Eh). The method is related to the single-set variational multi-configuration Gaussian approach (vMCG) but has the advantage that only a single quantum chemistry computation is required at each time step since there is only a single time-dependent potential surface. Therefore this removes the need for the diabatization procedure used in direct dynamics vMCG calculations, allowing the study of systems with multiple states of interest.
- A. J. Jenkins, K. E. Spinlove, M. Vacher, G. A. Worth, M. A. Robb, “The Ehrenfest method with fully quantum nuclear motion (Qu-Eh): Application to charge migration in radical cations” J. Chem. Phys., 149, 094108 (2018) https://doi.org/10.1063/1.5038428 PDF Supplementary

